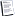Формальная производная полинома над полем GF(p^m)
В свое время я в теме, посвященной алгебраической теории кодирования,
обсуждал вопрос теоретического обоснования формулы формальной произ-
водной полинома L(x), приводимой в литературе по теории кодирования без
какого-либо выведения или хотя бы пояснений, и я изложил свою "версию"
вывода формулы, но тогда я ограничивался полиномами, конкретно над по-
лями Галуа GF(2^m), а теперь доразобрался и для общего случая GF(p^m).
Кстати говоря, полученная формула конечно похожа на ту, кот. приводится
в книге Ван дер Вардена, но в конечных полях GF(p^m) есть особый нюанс.
Если коротко, пусть задан полином L(x) = L[0] + L[1]*x + ... + L[k-1]*x^(k-1)
над конечным полем GF(p^m). Тогда формальная производная полинома L(x):
d(L(x))/dx = (L[1]*(1 mod p)) + (L[2]*(2 mod p))*x + ... + (L[k-1]*((k-1) mod p))*x^(k-2)
Особо обращаю внимание, что выражение (i mod p) для каждого i = 1...k-1
вычисляется в привычной арифметике, то есть берется остаток от деления
индекса i на простое число p. Но вот результирующий вычисленный остаток
интерпретируется как элемент поля GF(p^m), и далее вычисляется произве-
дение этого элемента на соответствующий коэффициент L[i], также являю-
щийся элементом поля GF(p^m) с использованием операции умножения поля.
Нюансом в конечным полях Галуа GF(p^m) является арифметическое свойство:
Сумма из n слагаемых элементов a: (a + a + ... + a) в поле равна ((n mod p)*a),
где (n mod p) вычисляется в привычной арифметике, а затем полученный оста-
ток интерпретируется как элемент поля GF(p^m) и умножается на элемент a с
использованием уже операции умножения этого поля. Именно этот нюанс лежит
в основе вывода формулы формальной производной L(x). Подробности в файле.
|