Цитата:
Сообщение от IvanSpbRu
Уточню: про неразрешимость алгебраического уравнения степени выше 4 в радикалах я в курсе
|
Ну извиняйте! Каков вопрос, таков и ответ. Телепаты все в отпуске, и откуда мне знать, что вам
Цитата:
Сообщение от IvanSpbRu
хочется надеяться на наличие такой явной приближенной формулы
|
?
Ладно, хотите приближенную - будет вам приближенная. Берем уравнение из поста №3. Преобразуем его к такому виду:
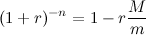
Левую часть раскладываем в степенной ряд в окрестности нуля. Я выпишу только четыре слагаемых.
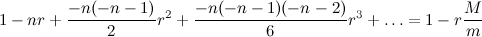
Единица (о, счастье!) сокращается. Случай
r=0 мы не рассматриваем, поэтому на
r можно смело поделить левую и правую части.
Я удержу слева только два слагаемых. Если не хватит точности, можете оставить и третье, но тогда придется решать квадратное уравнение. Итак,
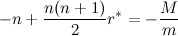
где
r* - приближенное решение, откуда получаем
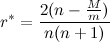
Несколько замечаний:
1)
r - это доля, т.е., например, для 10% будет
r=0,1;
2) я мог налажать с арифметикой, поэтому - просьба проверить выкладки;
3) следует помнить, что в исходной формуле вид процента определяется периодичностью выплат. Если например, платежи совершаются через год, тогда
r - это процент годовых, а если через месяц, тогда - процент месячных (гусары, молчать!!111). Поэтому и плясать надо от периодичности выплат (раз в месяц), а итоговый пересчет месячных в годовые в большинстве случаев - банальное умножение на 12 (т.е. простые проценты);
4) для контроля точности можно посчитать невязку: снести в одну сторону слагаемые из поста №3 и подставить
r* в получившееся соотношение. Ясно, что нулю оно уже равно не будет, но велико ли отклонение от нуля? Это даже интересно.
В принципе,
r - число маленькое, степень его убывает быстро, поэтому точности должно хватить.
Так что пользуйтесь на здоровье! Если не будет работать - пишите, доработаем напильником!