
 |
|
|
|
#1 |
|
Honorary Platinum Member
Регистрация: 28.10.2006
Сообщений: 10,479
|
Коллеги,
Есть ли формулы, выражающие в явном виде ставку процента при заданной сумме кредита, величине аннуитетного платежа и совокупном числе платежей? Рассчитать платеж при заданной ставке и прочих параметрах - не проблема. А вот тут интересует обратная задача - найти ставку по величине платежа. У Четыркина ничего не нашел... |
|
|

|
| Реклама | |
|
| |
|
|
#2 |
|
Silver Member
Регистрация: 12.01.2011
Сообщений: 913
|
Это можно сделать в Excele. Размещаете процентную ставку, сумму кредита, число платежей в отдельных ячейках. Используя эти ячейки, считаете величину платежа по формуле ПЛТ(...). Для обратного решения используете опцию "поиск решения" (вкладка Данные в Excel 2007, для активации Параметры Excel --> Надстройки --> Поиск решения): целевая ячейка - величина платежа, задаете конкретное значение, изменяемая ячейка - процетная ставка.
Последний раз редактировалось Kayra; 12.05.2012 в 11:42. |
|
---------
Исследовать - значит видеть то, что видели все, и думать так, как не думал никто. (А. Сент-Дьёрдьи)
|
|
|
|

|
|
|
#3 | |
|
Advanced Member
Регистрация: 22.12.2010
Адрес: Московская область
Сообщений: 320
|
Цитата:
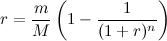 где M - сумма (тело) кредита, m - величина аннуитетного платежа, n - число выплат. Видно, что степень уравнения равна n+1. Для n<=3 - еще туда-сюда, по формуле Кардано и т.п. (для извращенцев). Если число платежей больше, то решение в общем случае можно найти только численно (например, методом Рунге-Кутты). Именно это |
|
|
|

|
|
|
#4 |
|
Platinum Member
Регистрация: 22.07.2010
Адрес: Санкт-Петербург
Сообщений: 3,304
|
|
|
---------
DNF is not an option
|
|
|
|

|
|
|
#5 |
|
Honorary Platinum Member
Регистрация: 28.10.2006
Сообщений: 10,479
|
Спасибо, коллеги.
Уточню: про неразрешимость алгебраического уравнения степени выше 4 в радикалах я в курсе  Но при этом есть вполне себе удобная приближенная формула для расчета IRR (где тоже, как правило, степень выше 4). Вот мне хочется надеяться на наличие такой явной приближенной формулы и для ставки. Увы, видимо надежды беспочвенные... Но при этом есть вполне себе удобная приближенная формула для расчета IRR (где тоже, как правило, степень выше 4). Вот мне хочется надеяться на наличие такой явной приближенной формулы и для ставки. Увы, видимо надежды беспочвенные...
|
|
|

|
|
|
#6 | |
|
Advanced Member
Регистрация: 22.12.2010
Адрес: Московская область
Сообщений: 320
|
Цитата:
? Ладно, хотите приближенную - будет вам приближенная. Берем уравнение из поста №3. Преобразуем его к такому виду: 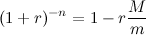 Левую часть раскладываем в степенной ряд в окрестности нуля. Я выпишу только четыре слагаемых. 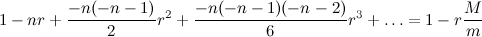 Единица (о, счастье!) сокращается. Случай r=0 мы не рассматриваем, поэтому на r можно смело поделить левую и правую части. Я удержу слева только два слагаемых. Если не хватит точности, можете оставить и третье, но тогда придется решать квадратное уравнение. Итак, 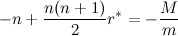 где r* - приближенное решение, откуда получаем 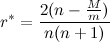 Несколько замечаний: 1) r - это доля, т.е., например, для 10% будет r=0,1; 2) я мог налажать с арифметикой, поэтому - просьба проверить выкладки; 3) следует помнить, что в исходной формуле вид процента определяется периодичностью выплат. Если например, платежи совершаются через год, тогда r - это процент годовых, а если через месяц, тогда - процент месячных (гусары, молчать!!111). Поэтому и плясать надо от периодичности выплат (раз в месяц), а итоговый пересчет месячных в годовые в большинстве случаев - банальное умножение на 12 (т.е. простые проценты); 4) для контроля точности можно посчитать невязку: снести в одну сторону слагаемые из поста №3 и подставить r* в получившееся соотношение. Ясно, что нулю оно уже равно не будет, но велико ли отклонение от нуля? Это даже интересно. В принципе, r - число маленькое, степень его убывает быстро, поэтому точности должно хватить. Так что пользуйтесь на здоровье! Если не будет работать - пишите, доработаем напильником! |
|
|
|

|
|
|
#7 |
|
Honorary Platinum Member
Регистрация: 28.10.2006
Сообщений: 10,479
|
|
|
|

|
|
|
#8 |
|
Advanced Member
Регистрация: 22.12.2010
Адрес: Московская область
Сообщений: 320
|
Дабы юные математики прониклись красотой решения из поста №6, для сравнения предлагаю "лобовой" путь получения другого приближения для r*. Исходную формулу переписываем в виде
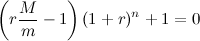 Вторую скобку раскладываем по формуле бинома Ньютона: 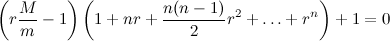 Чтобы линейно выразить отсюда приближенное значение r, я вынужден пожертвовать всеми членами разложения, кроме первых двух. Видно, что из бинома отхвачен довольно значительный кусок. В предыдущем же варианте мне удалось сохранить даже вторую степень r, а в силу знакопеременности ряда модуль его остатка не превышает абсолютного значения четвертого члена (того, в котором куб r) - это по признаку Лейбница. Теперь вопрос: какой вариант точнее? |
|
|

|